BLOQUE I: Operaciones con distintos tipos de funciones

Características matemáticas que definen las relaciones entre dos magnitudes enfatizando las de carácter funcional  

Funciones

En matemáticas, una función es el término usado para indicar la relación o correspondencia entre dos o más cantidades. Por ejemplo: el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A=π·r²

Todas las funciones se clasifican necesariamente dentro de uno de los dos conjuntos infinitos de funciones, que son:

• Conjunto de funciones elementales, formadas por los polinomios, el cociente de polinomios, los radicales, las funciones trigonométricas y sus inversas, las funciones exponencial y logarítmica, así como todas las funciones formadas a partir de las anteriores mediante operaciones algebraicas o composición de funciones.
• Conjunto de funciones no-elementales, son el resto de funciones, es decir, cualquier función que no puede ser obtenida mediante un número finito de pasos combinando funciones elementales es una función no elemental.

Una función puede venir dada en forma explícita o en forma implícita. Una fórmula explícita tiene la forma:

que permite calcular directamente el valor de y dado el valor de x. Por el contrario una función está en forma implícita si la variable dependiente no está explicitada respecto a la variable independiente, expresándose de la forma:

Una función puede representarse de diversas formas: mediante el citado algoritmo para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen, o como una gráfica que dé una imagen de la función.

Ejemplo 1

Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos

Conjunto X	Conjunto Y
Magali	55
Jonathan	68
Renata	52
Adrián	78
Carlos	60

Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso.

con esta explicacion vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto(X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento en X sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y.

Dominio y rango de una función

El rango es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.

Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.

Por ejemplo la función f(x) = 3x² – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función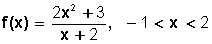   tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.

En el caso de la función 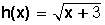 , el dominio de esta función son todos los números reales mayores o iguales a –3, ya que  x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.